10. Area and Average Value
a. Area Below a Curve
You already know how to solve problems of the following type:
Find the area below a positive function \(y=f(x)\) above the \(x\)-axis between \(x=a\) and \(x=b\).
Recall that this area is the integral: \[ A=\int_a^b f(x)\,dx \] However, you should also recall the derivation of this formula, since it is the model for all the other applications of integration.
The formula for the area is derived by slicing up the region into \(n\) rectangles each of width \(\Delta x=\dfrac{b-a}{n}\) and height \(f(x_i^*)\) where \(x_i^*\) is a point in the \(i^\text{th}\) interval \([x_{i-1},x_i]\).
The area is then obtained by adding up the areas of the rectangles and taking the limit as the number of rectangles becomes large, (\(n\to\infty\)): \[ A=\lim_{n\rightarrow\infty}\sum_{i=1}^n f(x_i^*)\Delta x \] This limit of a sum is recognized as the integral \(\displaystyle A=\int_a^b f(x)\,dx\).
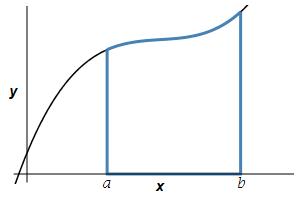
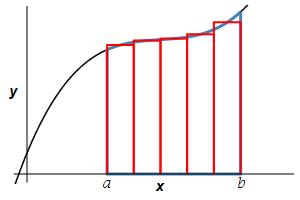
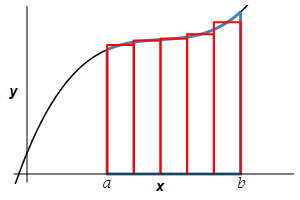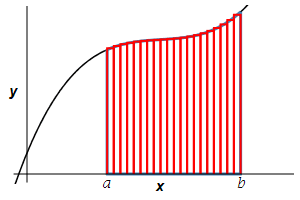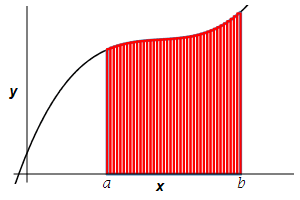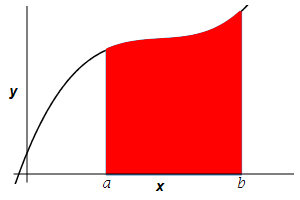
The area below a positive function \(y=f(x)\) above the \(x\)-axis between \(x=a\) and \(x=b\) is \[A=\int_a^b f(x)\,dx\]
Find the area below the curve \(y=x(x-3)^2\) and above the \(x\)-axis between \(x=0\) and \(x=3\).
The area is \[\begin{aligned} A&=\int_0^3 x(x-3)^2\,dx \\ &=\int_0^3 (x^3-6x^2+9x)\,dx \\ &=\left[\dfrac{x^4}{4}-2x^3+\dfrac{9}{2}x^2\right]_0^3 =\dfrac{27}{4} \end{aligned}\]
^2.jpg)
Now try it yourself:
Plot the parabola \(y=9-x^2\) and find the area below the parabola above the \(x\)-axis.
Find the limits by solving \(9-x^2=0\).
\(\displaystyle A=\int_{-3}^3 (9-x^2)\,dx=36\)
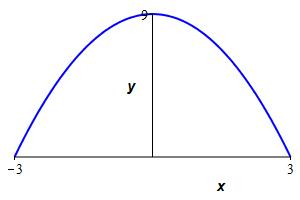
To find the limits on the integral, we solve the equation \(9-x^2=0\) to get \(x=-3,3\). So the area is \[\begin{aligned} A&=\int_{-3}^3 (9-x^2)\,dx =\left[9x-\dfrac{x^3}{3}\right]_{-3}^3 \\ &=(27-9)-(-27+9) =36 \end{aligned}\]

Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum